png，252x312，7446b

数形结合:b,c不对._ 故选a._ 本题主要考查函数零点的应用,根据函数和方程之间的关系构造函数g(t),利用数形结合是解决本题的关键.难度较大._ 当-2≤t\u003C-1,即:m-2\u003Cx\u003Cm-1,[t]=-2,此时g(t)=$-\\frac{2}{t}$

,"height":384x512，6251b

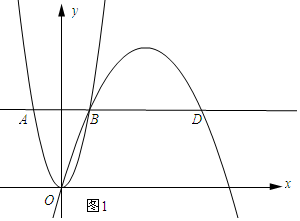
0),b(x2,0),(x1(1)求a,b的值;(2)分别求出直线ac和bc的解析式;(3)若动直线y=m(0图..._ 已知抛物线y=ax^2+bx+2与x轴相交于点a(x1,0),b(x2,0),(x1(1)求a,b的值; (2)分别求出直线ac和b

jpg，454x546，36212b

如果存在m点, 所以,所以a点为(4, 所以, 则m为(3;4), g(x)=ax+3, 又因为ac过a点, a点也在x轴上, x1=1, 9/4+3x=9//, 因为n点在x轴上, 所以d点的坐标为(1, 9/

jpg，350x571，30568b

12.已知一次函数y=(2m-3)x+(2+n)_ (1)当m为何值时,y随x增大而减小._ (

png，221x300，5422b

∵点b的横坐标为m,ab=2m,bd=2ab,_ ∴点d的横坐标为5m._ ∴过点o、b、d三点的抛物线的对称轴为x=3m._ ∴经过b、c且顶点在x轴上的抛物线的对称轴为x=$\\frac{3}{2}$m._ ∴抛物线的对称轴为x=3._ ∴经过

jpg，286x444，9383b

方法2_ b=3-a代入_ ∴动点m(a,b)在直线x+y=3即x+y-3=0上_ 式子(a+5)^2+(b-2)^2表示动点m(a,b)_ 到定点a(-5,2)的距离|ma|的平方.

png，212x214，5792b

∴设m(t,-$\\frac{4}{3}$t+8),_ ∵以c,d,m,n为顶点的四边形是平行四边形,_ ∴有cd为边和cd为对角线两种情况,_ ①当cd为边时,则mn∥cd,且mn=cd=4,_ 当m、n在x轴上方时,如图2,则n点坐标为(t+4,

png，268x395，17752b

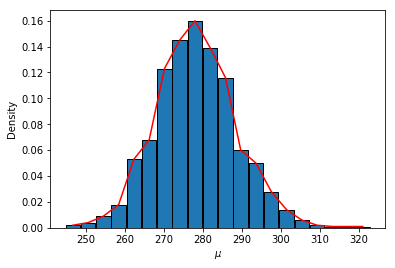
gibbs 抽样_ 定义_ , 在gibb抽样中, 称_ 为_ 的满条件分布, 其中_ . 假设这_size=1000) #从自由度n-1的卡方分布中抽取y, 并解出对于的sigma^2_ mus = stats.norm.rvs(x_m

jpg，1406x981，232977b

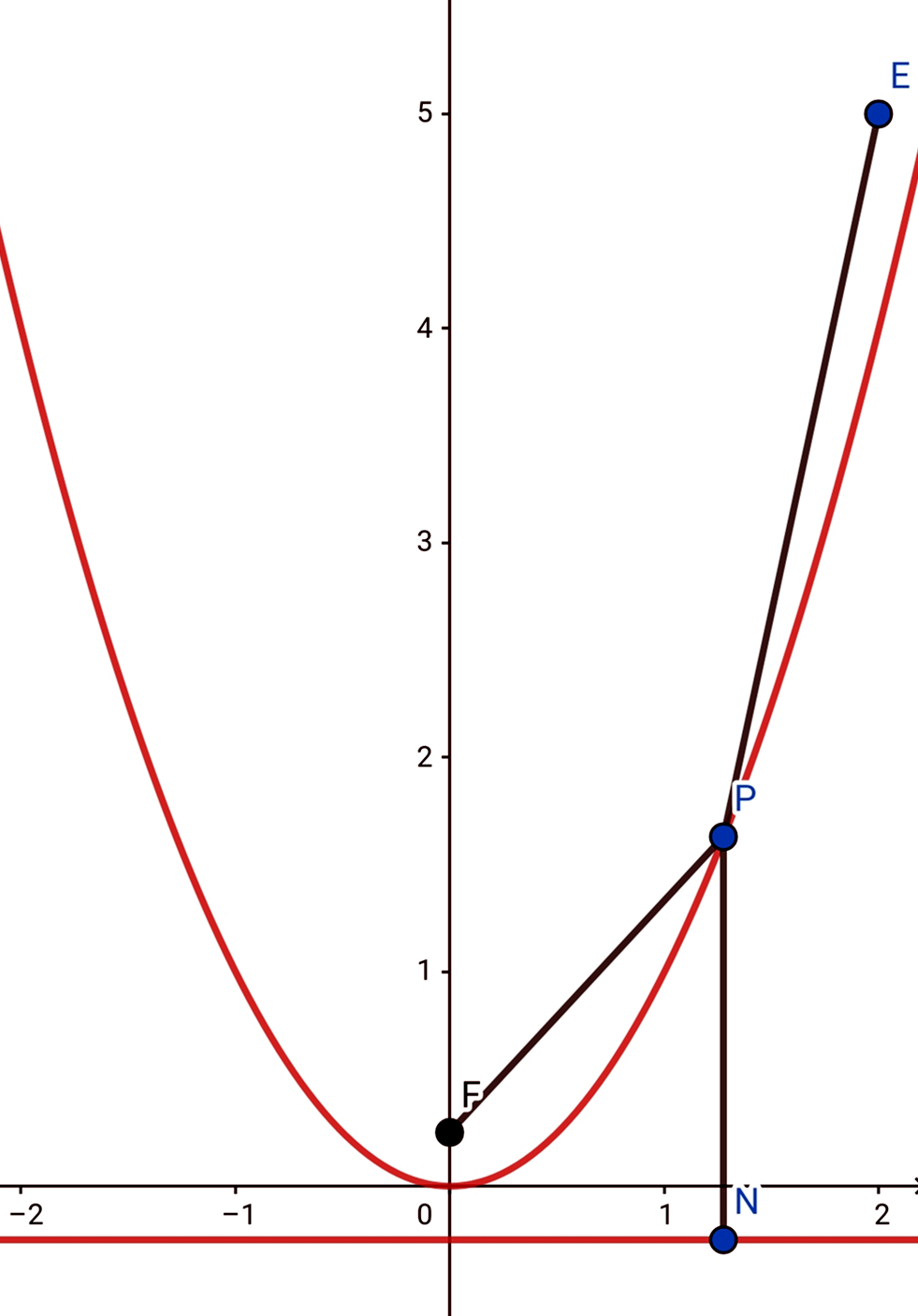
1)求二次函数的解析式_ (2)直角坐标系中有一点e(2,5),试问当动点p位于何处时,pe+pf有最小值,并求出最小值_ 解析:_ (1)y=x^2,过程略_ (2)设p(m,n)其中n=m^2_ [2013年浙江省一级中点中学自主招生卷]-

jpg，232x500，30170b

这个图怎么画出来的_ 已知函数f(x)满足f(x)+1=1/f(x+1),当x∈[0,1]时,f(x)=x;若在区间(-1,1)内,g(x)=f(x)-mx-m有两个零点

,"height":480x480，318105b

labs(title =\"年份: {frame_time}\",x =\"每个国家的gpd\", y =\"每个国家的寿命\")+_ 首先绘制一张静态图,以gdp为x轴

jpg，257x347，9424b

当直线z=2x+3y过平行域上点m时,截距最小,z最小.解方程_ 得m点坐标为(5,5)._ 此时z_ 答:两种金属板各取5张时,用料面积最省._ 解:设a、b两种金属板各取x张、y张,用料面积为z,则约束条件是_ 目标函数是z=2x+3y,